ミクロなスケールでの現象を記述する量子論・場の量子論の研究,特に素粒子を記述するゲージ場の量子論の研究を行っています.また,研究で得られた知見を物性系を含む身近な現象に応用する研究も行っています.一方,博士前期課程までの研究課題としては理論物理学の広範な内容を扱っています.
メンバー
研究指導委託教員 三角樹弘 (近畿大学理工学部准教授)
D1 湯本純
M2 湯川大地
M1 千頭和裕之 津金澤大
OB 2020年度修了 崔 粲 (東北大学大学院進学)
2019年度修了 小原 賢 (株式会社 電力計算センター)
2019年度修了 塚本尚輝 (プログレス・テクノロジーズ株式会社)
2019年度卒業 柳田龍之介(航空自衛隊)
2018年度修了 高畑 結 (ローランド株式会社)
2018年度卒業 奥山健人 (PwCあらた有限責任監査法人)
2016年度卒業 李 韜瀚 (東北大学大学院進学)
修士論文研究課題
2020年度
「位相幾何学的手法に基づく格子上のカイラルゲージ理論と 大統一理論の構成」
2019年度
「一般の場の量子論と重力理論についてのゲージ/重力対応」
「場の量子論における真空エネルギーとカシミール効果の解析法」
2018年度
「高次摂動計算に基づく量子トンネル効果の解析」
卒業論文研究課題
2020年度
「量子テレポーテーション」
「一般相対性理論とブラックホール解」
「物理学におけるリー代数」
2019年度
「均一磁場中スピン1/2系の量子論的歳差運動」
「特殊相対論の基礎」
「マクスウェル方程式の相対論的定式化」
2018年度
「素粒子物理学におけるリー群」
「量子情報通信における非局所性とベルの不等式」
2017年度
「量子力学の非局所性とベルの不等式」
「一般相対性理論と重力波の検出原理」
2016年度
「経路積分法と摂動計算に基づく量子系の解析」
研究内容
1.量子論における摂動計算と複合ソリトン配位との関係(リサージェンス理論)微小世界を記述する量子論においては,しばしば摂動計算と呼ばれる漸近展開に基づく計算手法が用いられます.特に素粒子現象を記述する場の量子論では大変重要になりますが,摂動級数は一般に発散するため,大部分のパラメータ領域の解析が出来ません.近年,その発散が実は摂動計算では記述出来ないとされる「非摂動現象」の情報を含む可能性(リサージェンス構造)が指摘されています.本研究室では,量子力学系,2次元シグマ模型,3次元超対称チャーン・サイモン理論,4次元QCD型理論について摂動級数と非摂動効果との関係を調べています. 関係する主要な業績 |
図1 |
2.コンパクト化時空上のゲージ理論の相構造と閉じ込めコンパクト化された次元を持つ空間に定義されたゲージ理論においてはしばしばゲージ対称性の自発的破れ等の興味深い現象が生じるだけでなく,コンパクト化半径が十分小さい場合には解析が容易になる,という特性があります.本研究室では,このような理論の相構造特に閉じ込めについての相構造を調べ,現実の強い力を記述するゲージ理論(QCD)とどのように繋がるかを調べています.特に近年は,量子異常マッチングと呼ばれる手法を用いた相構造の解析手法が注目を集めており,その手法に基づくQCD型理論や2次元シグマ模型の相構造研究を進めています. 関係する主要な業績 |
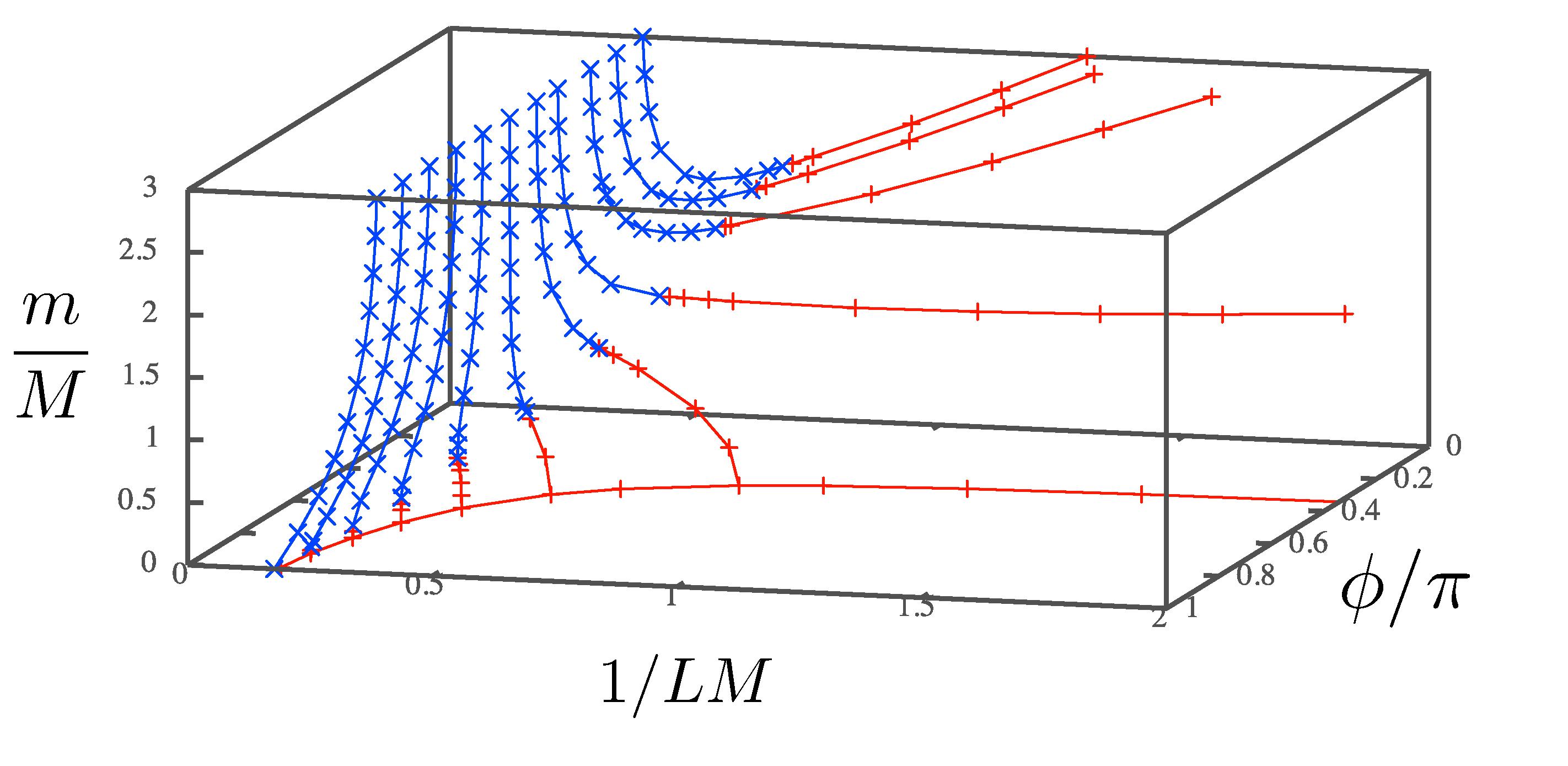
図2 |
3.離散化された時空における超対称ゲージ理論の厳密解と数値計算超対称ゲージ理論は高い対称性を持つため性質が良く,ある種の物理量については厳密に解ける場合もあります.本研究室では一般の離散化時空における超対称ゲージ理論について厳密解の導出と数値計算を行うことで,曲がった時空における超対称理論の性質を調べています. 関係する主要な業績 |
図3 |
4.新しい格子離散化法やQCD型模型の格子シミュレーション摂動論を超える場の量子論解析法の一般的枠組みの1つとして格子ゲージ理論があります.この理論では時空間を離散化し,格子点やそれらを繋ぐ線上に自由度を定義します.解析計算はこの場合も難しいですが,モンテカルロ法と呼ばれる統計的手法を用いた数値計算が有効であり,多くの成果を上げています.一方,離散化の結果として重大な問題が生じることや,現実の素粒子理論の解析が困難なこともあります.本研究室ではこの問題点を解消し得る格子模型を提案や,現実の素粒子理論とは少し異なる理論の数値シミュレーションを行っています. 関連する主要な業績 |
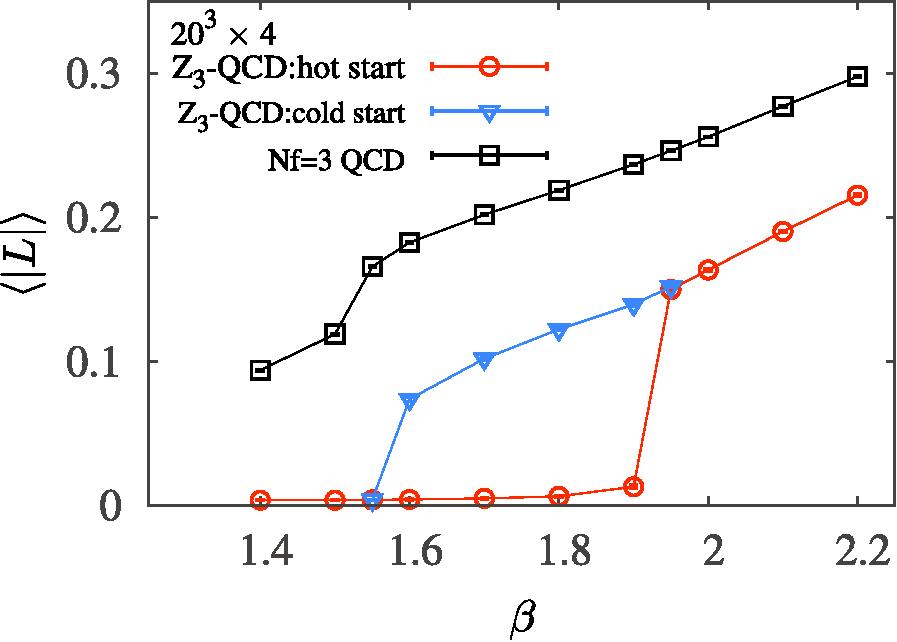
図4 |
5.場の理論的観点に基づく物性模型の研究物性系は場の量子論で記述される身近な例であり,物性理論は上記のような研究成果を活かすことができる分野です.中でも近年注目を集めるようになったグラフィン系やトポロジカル絶縁体と言われる物質は,場の量子論の知識を用いることで理解が大いに進みました.本研究室では,ハニカム格子模型や平坦バンド模型と呼ばれる物性模型に注目し,模型の一般化,トポロジカルな性質の研究,電磁応答の解析などを行っています. 関連する主要な業績 |
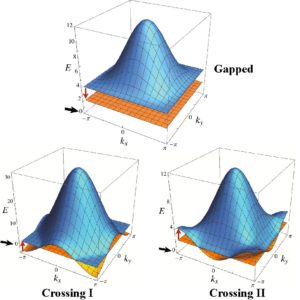
図5 |
6.ホログラフィック模型に基づく場の量子論の非摂動的解析場の量子論の非摂動的側面を理解する方法として,ゲージ重力対応を用いる手法があります.超弦理論を考えると,ある種のゲージ場の量子論と重力理論が等価性を持つことが予想され,その予想に基づいて構成されたゲージ理論に対応する重力模型をホログラフィック模型と呼びます.本研究室では,このような模型を用いた有限温度QCD系の解析を行っています. 関連する主要な業績 |
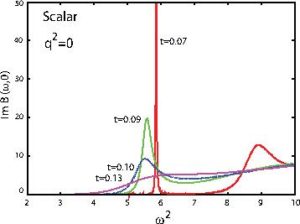
図6 |
教員メッセージ
世の中で起きている物事は多種多様で予想がつきません。しかし、この宇宙で起きるすべての物事は、例えそれが人間の意思に基づくとしても、何らかの法則に従って起きていると考えられます。人間の体を形作る細胞はより詳しく見るとアミノ酸の集合体ですが、さらに細かく見ると分子・原子から出来ており、それらの振る舞いは「量子論」とよばれる”小さい”物の動きを司る法則に従っています[図7参照]。一方、宇宙空間において星やそれを包含する銀河の振る舞いは「一般相対性理論」とよばれる”大きい”物の動きを司る法則に従っています[図7参照]。ですので、社会現象や自然災害も、究極的にはこれらの2つの法則の結果として生じていると考えられます。
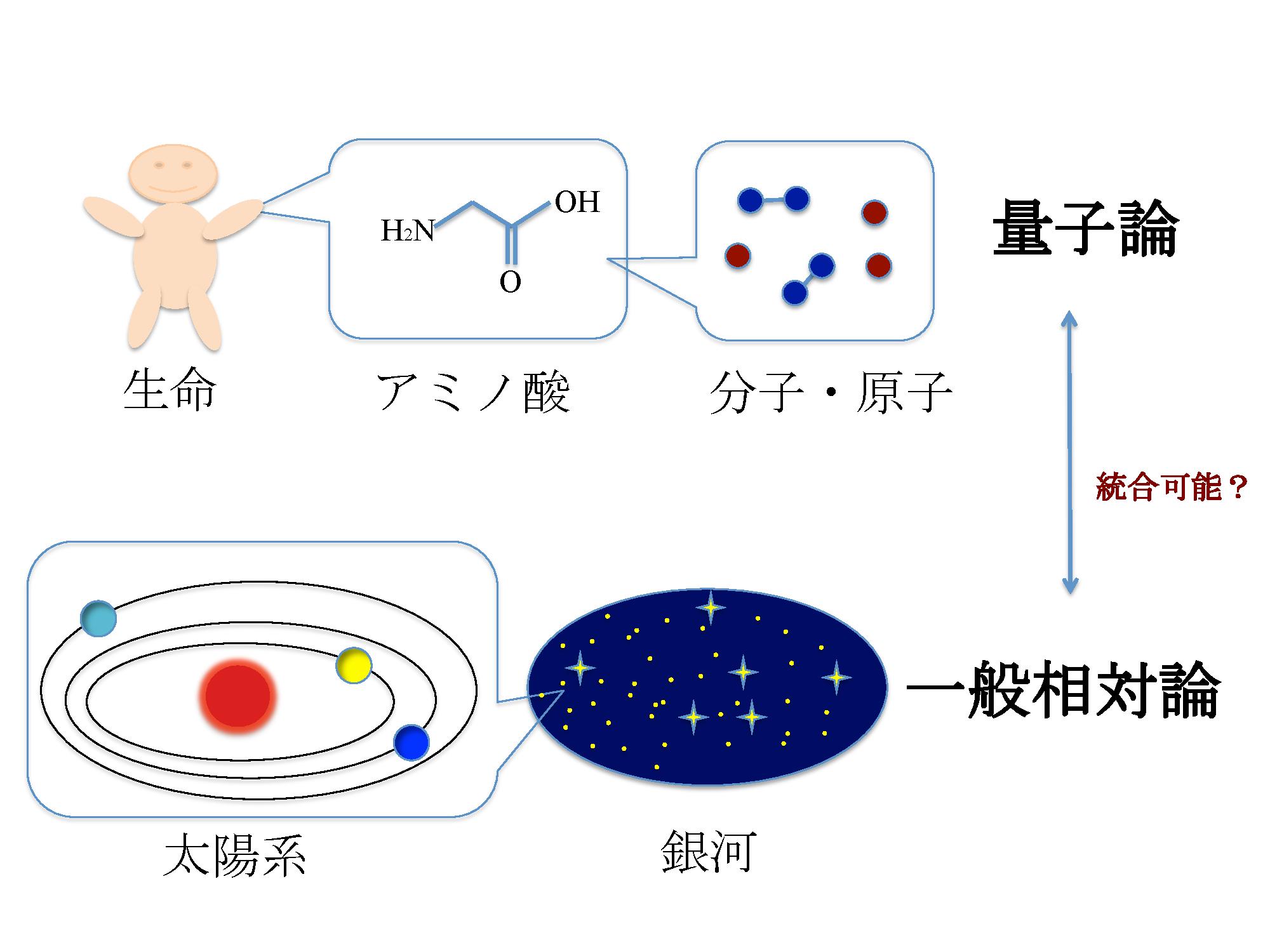
図7
この話で注目してほしいのは、物事の規模によって主立つ法則が異なる点です。実は、素粒子物理学と呼ばれる分野の研究者は、一見異なるように見えるこれら2つの法則も実は1つの共通の法則の異なる見え方だと考えています。そしてその法則はたった一つの単純な方程式で記述されるだろうと。このような法則あるいは方程式は「万物の理論」(Theory of Everthing)と呼ばれ、宇宙で起きるの出来事はこの一つの方程式に基づいていると期待されます。
このように自然現象の背景には普遍的な規則が存在するはずで、その規則を記述する単純な方程式は何か、という謎が物理学の一つの問いです。一方、どうしてたった1つの方程式から大宇宙が生まれ、生命が生まれ、人間の思考が形成されるのか、というように多様性が生み出される理由を考えるのも物理学の魅力的な問いです。このような数学を用いた自然の真理の探求に興味のある人は、是非ともこの分野に飛び込んで来てください。
三角樹弘
業績一覧や研究歴などは以下を参照してください.
Researchmap http://researchmap.jp/misumi/
Google scholar https://scholar.google.com/citations?user=rJNI3UIAAAAJ&hl=en
inSPIRES http://inspirehep.net/author/profile/T.Misumi.1?ln=ja